- UID
- 468
- UCC
-
- 声望
-
- 好评
-
- 贡献
-
- 最后登录
- 1970-1-1
|
 发表于 2008-5-16 20:22:01
|
显示全部楼层
发表于 2008-5-16 20:22:01
|
显示全部楼层
好吧,不是百度的
Parsec
Jump to: navigation, search
For other uses, see Parsec (disambiguation).
See 1 E+16 m for comparable lengths, and scientific notation for an explanation of the notation used in this article.
1 parsec =SI units30.8568×1012 km30.8568×1015 mAstronomical units206.265×103 AU3.2616 lyUS customary / Imperial units19.1735×1012 mi101.236×1015 ft
 
A parsec is the distance from the Earth to an astronomical object which has a parallax angle of one arcsecond.
The parsec (symbol pc) is a unit of length used in astronomy. The length of the parsec is based on the method of trigonometric parallax, one of the oldest methods for measuring the distances to stars.
The name parsec stands for "parallax of one second of arc", and one parsec is defined to be the distance from the Earth to a star that has a parallax of 1 arcsecond. The actual length of a parsec is approximately 3.086×1016 m, 3.262 light-years or 19,176,075,967,324.937 miles.
[edit] HistoryThe first direct measurements of an object at interstellar distances were undertaken by German astronomer Friedrich Wilhelm Bessel in 1838, who used the width of the Earth's orbit as a baseline to calculate the distance of 61 Cygni using parallax and trigonometry.[1] The parallax of a star is half of the angular distance a star appears to move relative to the celestial sphere as Earth orbits around the Sun; or, reciprocally, it is the angle subtended, from that star's perspective, by the semi-major axis of the Earth's orbit. The use of the parsec as a unit of distance follows naturally from this method, since distance (in parsecs) is simply the reciprocal of the parallax angle (in arcseconds). That is, it is the distance at which the semi-major axis of the Earth's orbit would subtend an angle of one second of arc. (See diagram above.)
Though it had probably been used before, the term parsec was first mentioned in an astronomical publication in 1913, when Astronomer Royal Frank Watson Dyson expressed his concern for the need of a name for that unit of distance: he proposes the name astron, but mentions that Carl Charlier had suggested siriometer, and Herbert Hall Turner had suggested parsec (par-allax sec-ond).[2]
[edit] Usage and MeasurementThe parallax method is the fundamental calibration step for distance determination in astrophysics, and the natural unit for such measurements, the parsec, has become the most commonly used unit of distance in scholarly astronomical publications. Articles aimed at a wider audience, such as in newspapers and popular science magazines, often use a more intuitive unit, the light-year (ly).
Other than the Sun, which has a parallax of 90 degrees, there is no known star whose parallax is more than 1 arcsecond (that is, there is no known star whose distance from Earth is less than 1 parsec). The next closest star is Proxima Centauri with a parallax of 0.77233 arcseconds; it is thus 1.295 pc (4.225 ly) away from the Earth.
Refraction caused by the atmosphere, also known as astronomical seeing, limits ground-based telescopes to parallax angle measurement accuracies of less than approximately 0.01 arcsec,[citation needed] so reliable measurements, those with errors of 10% or less, can only be achieved at stellar distances of no more than about 100 pc, or 326 ly. Space-based telescopes are not limited by this effect and can accurately measure distances to objects beyond the limit of ground-based observations.
Between 1989 and 1993, the Hipparcos satellite, launched by the European Space Agency (ESA), measured parallaxes for about 100,000 stars with an astrometric precision of about 0.97 milliarcseconds, and obtained accurate measurements for stellar distances of stars up to 1,000 pc away.[3] NASA's FAME satellite was due to be launched in 2004, to measure parallaxes for about 40 million stars with sufficient precision to measure stellar distances of up to 2,000 pc. However, the mission's funding was withdrawn by NASA in January 2002.[4] ESA's GAIA satellite, due to be launched in December 2011, is intended to measure one billion stellar distances to within 20 microarcseconds, producing errors of 10% in measurements as far as the Galactic Center, about 8,000 pc away in the constellation of Sagittarius.[5]
[edit] Distances in parsecs
[edit] Distances less than a parsecDistances measured in fractions of a parsec usually involve objects within a single star system. So, for example:
[edit] Parsecs and kiloparsecsDistances measured in parsecs include distances between nearby stars, such as those in the same spiral arm or globular cluster. A distance of one thousand parsecs (approximately 3,262 ly) is commonly denoted by the kiloparsec (kpc). Astronomers typically use kiloparsecs to measure distances between parts of a galaxy, or within groups of galaxies. So, for example:
- one parsec is approximately 3.262 light-years.
- the nearest known star to the Earth, other than the Sun, is Proxima Centauri, 1.29 parsecs away.
- the center of the Milky Way is about 8 kpc from the Earth, and the Milky Way is about 30 kpc across.
- the Andromeda Galaxy (M31), the most distant object visible to the naked eye, is a little under 800 kpc away from the Earth.
[edit] Megaparsecs and gigaparsecsA distance of one million parsecs (approximately 3,262,000 ly or 2×1019 miles) is commonly denoted by the megaparsec (Mpc). Astronomers typically measure the distances between neighboring galaxies and galaxy clusters in megaparsecs.
Galactic distances are sometimes given in units of Mpc/h (as in "50/h Mpc"). h is a parameter in the range [0.5,0.75] reflecting the uncertainty in the value of the Hubble constant for the rate of expansion of the universe (H = 100h km/s/Mpc). The Hubble constant becomes relevant when converting an observed redshift z into a distance using the formula d ≈ c / Hz (where c is the velocity of light).[6]
One gigaparsec (Gpc) is one billion parsecs — one of the largest distance measures commonly used. One gigaparsec is about 3.262 billion light-years, or roughly one fourteenth of the distance to the horizon of the observable universe (dictated by the cosmic background radiation). Astronomers typically use gigaparsecs to measure large-scale structures such as the size of, and distance to, the Great Wall; the distances between clusters of galaxies; and the distance to quasars.
For example:
[edit] Volume unitsIn order to determine the number of stars in the Milky Way Galaxy volumes in kpc3 (1 cubic kiloparsec ≈ 2.938 × 1058 m3) are selected in various directions. All the stars in these volumes are counted and the total number of stars is statistically determined. The number of globular clusters, dust clouds and interstellar gas is determined in a similar fashion.
In order to determine the number of galaxies in superclusters volumes in Mpc3 (1 cubic megaparsec ≈ 2.938 × 1067 m3) are selected. All the galaxies in these volumes are classified and tallied. The total number of galaxies can then be determined statistically. The huge void in Bootes[7] is measured in Mpc3.
In Cosmology volumes of Gpc3 (1 cubic gigaparsec ≈ 2.938 × 1076 m3) are selected to determine the distribution of matter in the visible universe and to determine the number of galaxies and quasars.
The Sun is alone in its cubic parsec (1 pc3 ≈ 2.938 × 1049 m3) but in globular clusters the stellar density per pc3 could be from 100 to 1,000.
[edit] Calculating the value of a parsec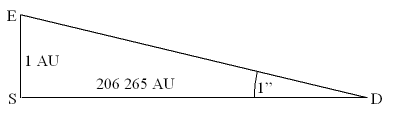
In the diagram above (not to scale), S represents the Sun, and E the Earth at one point in its orbit. D is a point in space at a distance of one parsec from the Sun. By definition, the angle D is one arcsecond, and the distance ES is one astronomical unit (AU). By trigonometry, the distance SD is
 One AU = 149,597,870,700 m, so 1 parsec ≈ 3.085 678×1016 meters ≈ 3.261 564 light-years. One AU = 149,597,870,700 m, so 1 parsec ≈ 3.085 678×1016 meters ≈ 3.261 564 light-years.
[edit] References
[edit] Notes^ Bessel, FW, "Bestimmung der Entfernung des 61sten Sterns des Schwans" (1838) Astronomische Nachrichten, Vol.16, p.65-96. ^ Dyson, F. W., "The distribution in space of the stars in Carrington's Circumpolar Catalogue" (1913) Monthly Notices of the Royal Astronomical Society, Vol. 73, p.334-342; see footnote on p.342. ^ The Hipparcos Space Astrometry Mission. Retrieved on August 28, 2007. ^ FAME news, 25 January 2002. ^ GAIA from ESA. ^ Galaxy structures: the large scale structure of the nearby universe. Retrieved on May 22, 2007. - ^ Astrophysical Journal, Harvard
[edit] See alsoRetrieved from "http://en.wikipedia.org/wiki/Parsec" |
|
 /1
/1 